So wie versprochen hier jetzt das Handout zu meinen Vortrag über die Zufallsgrößen. Die Aufgabe stammt aus dem Buch, welches als Quelle angegeben ist. Es wurde aber darauf geachtet das kein Text übernommen wird. Ich muss ja auch noch ein Versprechen einlösen und zwar den Link zu Baynado’s-Blog da er mir bei der Varianz geholfen hat.
… Weiterlesen “Zufallsgrößen und deren Wahrscheinlichkeitsverteilung….”Kategorie: Mathe
Vortrag Zufall und Wahrscheinlichkeit
Heute war ich, von der Schule aus, in einem Vortrag über Zufall und Wahrscheinlichkeit. Neben einigen Infos zur Entstehung der Wahrscheinlichkeitsrechnung gab es auch Beispiele für die Nutzung von Zufallsexperimenten.
Das Erste, was ich interessant fand, ist, dass man mit Zufallsexperimenten Flächen berechnen kann, zwar nur mit ungefähren Werten, aber für den Anfang ist das ja meist schon ausreichend. Wenn zum Beispiel bekannt ist, wie groß ein bestimmtes Quadrat ist, und in diesem Quadrat haben wir nun ein eigenes Grundstück, welches eine komische Form hat ;-), wo die Fläche eigentlich nur mit einer Integralrechnung berechnet werden kann, kann ein Näherungswert … Weiterlesen “Vortrag Zufall und Wahrscheinlichkeit”
Quantitative und Qualitative Merkmale?
Bestimmte Dinge haben bestimmte Merkmale, welche in der Statistik wichtig sind zu unterscheiden. Es gibt auf der einen Seite die Quantitativen Merkmale, welche sich noch in stetig und diskret unterscheiden. Beispiele dafür sind die Armlänge (quantitativ und stetig) und die Sparanlage(quantitativ und stetig). Auf der anderen Seite gibt es die Qualitativen Merkmale wie die Mathmatikzensur(qualitativ und ordinal) oder die Haarfarbe ( qualitativ und nominal).
Soweit, so gut! Aber wie unterscheide ich das jetzt? Wie ist welches Merkmal definiert? Würde mich hier über eure Denkanstöße freuen.… Weiterlesen “Quantitative und Qualitative Merkmale?”
Zufallsexperiment
Was versteht man unter einen Zufallsexperiment? Ein Zufallsexperiment wird so genannt wenn es folgende Dinge erfüllt:
- es müssen mindestens zwei Ergebnisse möglich sein
- diese Ergebnisse dürfen vor Ablauf des Experimentes nicht vorhersagbar sein
- es kann prinzipiell in gleicher Weise beliebig oft ablaufen
Partialbruchzerlegung mittels Koeffizientenvergleich
Letztens hatte ich euch die Partialbruchzerlegung mit Koeffizientenvergleich vorgestellt, da ich es als Vortrag in der Abendschule gehalten hatte. Nun würde ich euch gerne noch die Übungsaufgabe zur Verfügung stellen, die ich dann noch ausgeteilt habe. Die Lösungen könnt ihr dann bei mir Anfordern.
Runterladen könnt ihr die Aufgabe hier als PDF-Datei.
Denkt bitte dran das das Copyright bei mir liegt (Sven Buchien) Ihr dürft die Datei gerne verwenden, auch in Vorträgen und weiß ich wo, aber es wäre schön, wenn ihr dann kurz auf meine Seite hinweißen könntet.… Weiterlesen “Partialbruchzerlegung mittels Koeffizientenvergleich”
Partialbruchzerlegung mit Koeffizientenvergleich
| Als erstes müssen wir uns überlegen mit welcher Methode hier gearbeitet wird. Da der Nenner dieser Funktion aus Linearfaktoren besteht, kann man den Bruch sofort in zwei Partialbrüche umwandeln. Der Zähler der neuen Brüche wird
mit Koeffizienten gebildet. Daraus ergibt sich dann: Im weiteren Schritt müssen dann die Koeffizienten A und B bestimmt werden. Dies geschieht, indem ich die oben gebildeten Brüche erst einmal wieder zusammenfast. Als erste muss der Hauptnenner gebildet werden, ( am besten schaut ihr noch einmal nach den Bruchrechnungsregeln) dann wird der Zähler ausgeklammert. Nach dem Ausklammern fasst man die Koeffizienten mit x Anteil und die |
Volumenberechnung bei einen Rotationskörper
Nach dem ich heute einen Mathetest geschrieben habe (welchen ich auch wieder versaut habe), habe ich mal folgende Aufgabe berechnet. Und zwar geht es um Volumenberechnung bei einen Rotationskörper. Ohne die Aufgabe zu kennen, nehme ich erst einmal folgenden Ansatz für die Volumenberechnung:
V=Pi x ∫(f(x))²
Findet ihr gleich als erstes noch einmal unten auf dem Bild wo die Aufgabe berechnet ist. Als Ausgang gibt es nun die Funktion k(x)=x+1. Diese wird im Intervall I=[1;3] rotiert. Hierbei entsteht ein Rotationskörper von welchen man das Volumen berechnen kann.

Dieses Ergebnis kann man noch einmal überprüfen, wenn man sich die Formel für … Weiterlesen “Volumenberechnung bei einen Rotationskörper”
Nachtrag zur Matheklausur
Die Matheklausur ist doch nicht ganz ein Ausfall geworden. Fünf Noten-Punkte konnte ich doch irgendwie zusammen sammeln und somit ist es eine vier geworden. Das bedeutet, Klausur gerade so bestanden und doch noch eine Chance auf dem Zeugnis insgesamt eine zwei in Mathe zu bekommen.… Weiterlesen “Nachtrag zur Matheklausur”
Integral von e(-x) * sin(x)
Nachdem ich gestern ein paar Probleme hatte, habe ich mich hingesetzt und noch eine zweite Integralrechnung durchgeführt. Das ganze zieht diesmal so aus:

In der Vorletzten Zeile im Bild fehlt eine zwei vor dem Integralzeichen.
Um das ganze nun zu beweisen das es richtig ist, muss man von der Funktion
die Ableitung bilden. Die 1/2 vor der Klammer kann man erst einmal vernachlässigen, darf sie am Schluss aber nicht vergessen. (Faktorregel). Kommen wir also zu der Funktion zwischen den Klammern. Da ein Minus vorhanden ist, handelt es sich hier um zwei Funktionen und deshalb muss hier die Summenregel angewendet werden. … Weiterlesen “Integral von e(-x) * sin(x)”
Integration von x*ln(x)
Nachdem ich mir Stundenlang den Kopf zerbrochen habe was an meiner Integration falsch ist, habe ich nun verstanden, dass an dieser überhaupt nichts falsch ist. Sie sieht also folgendermaßen aus und stimmt so auch 😉 :
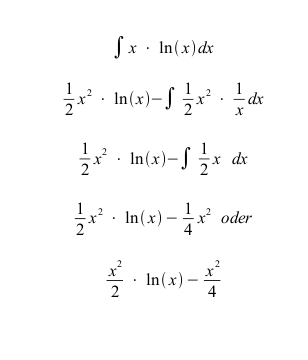
Was viel eher falsch war, war meine Methode die Ableitung zu bilden. Daher konnte ich nie auf die eigentliche Funktion, mit der ich begonnen hatte, zurückkommen. Ich habe mich aber jetzt im Netz mal ein wenig schlauer gemacht und mir die Ableitung bilden lassen. Das ganze ist Schritt für Schritt erklärt und sieht so aus:
| Summe ableiten: (f+g)‘ = f’+g‘ |
| Produkt ableiten: (f*g)‘ = |
