Nachdem ich gestern ein paar Probleme hatte, habe ich mich hingesetzt und noch eine zweite Integralrechnung durchgeführt. Das ganze zieht diesmal so aus:

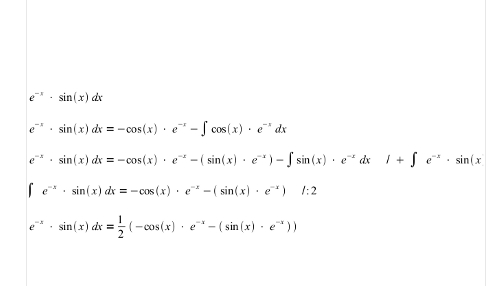
In der Vorletzten Zeile im Bild fehlt eine zwei vor dem Integralzeichen.

Um das ganze nun zu beweisen das es richtig ist, muss man von der Funktion

die Ableitung bilden. Die 1/2 vor der Klammer kann man erst einmal vernachlässigen, darf sie am Schluss aber nicht vergessen. (Faktorregel). Kommen wir also zu der Funktion zwischen den Klammern. Da ein Minus vorhanden ist, handelt es sich hier um zwei Funktionen und deshalb muss hier die Summenregel angewendet werden. Die Summen-Regel besagt das f'(x) + g'(x) gerechnet werden muss. Alles was in dieser Funktion vor dem Minus ist, ist also f(x) und was hinter dem Minus steht ist g(x). Da ein Minus das ganze trennt, wird das + in der Ableitungsregel zu einen Minus. Um nun von den beiden Funktionen die Ableitungen zu bilden, braucht man die Produkt-Regel. diese besagt (um gleich wieder ein paar neue Funktionen einzuführen 😉 ) das f'(x)=u'(x)*v(x)+u(x)*v'(x) ist. u(x) ist hierbei alles, was bei der Funktion f(x) vor dem mal steht und v(x) alles was dahinter steht. Für g'(x) gilt genau das selbe.

Wenn man diese Ableitungen nun alle durchführt und alles zusammenfast kommt man am Ende auf die Funktion:

Nun wissen wir aber, dass die zwei vor den Klammern zu viel ist, aber wir haben ja noch einen Drumpf in der Hand und zwar die 1/2 von vorhin, die welche vor der Klammer stand und die wir wegen der Faktorregen erst mal vernachlässigt haben. Rechnen wir nun 1/2 * 2 kommt 1 raus. Nun können wir die Klammern auflösen und kommen wieder auf die Ausgangsgleichung.