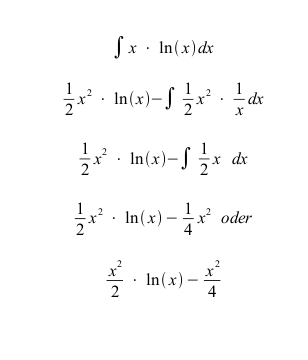Schlagwort: Ableitung

Veröffentlicht am
von

Ich wurde ja in einen anderen Beitrag durch einen Kommentator dazu aufgefordert x hoch x Abzuleiten. Bevor ich damit jetzt Anfange, zwei Anmerkungen. Mir wurde bei der Aufgabe nicht verboten Hilfe einzuholen, dass habe ich somit auch getan und zwar bei meiner Mathelehrerin die es uns daraufhin erklärt hat. Das zweite ist die Erklärung für dieses ^ – Zeichen. Immer wenn ihr das seht schreibe ich von Hoch, also x hoch etwas oder so 😉

f(x) = x^x

Diese Ausgangsgleichung wird jetzt so umgestellt, dass ich mit meinen Ableitungsregeln etwas anstellen kann. Das sieht dann aus wie folgt.

f(x) = … Weiterlesen “Ableitung von x hoch x”

Veröffentlicht am
von

Nachdem ich mir Stundenlang den Kopf zerbrochen habe was an meiner Integration falsch ist, habe ich nun verstanden, dass an dieser überhaupt nichts falsch ist. Sie sieht also folgendermaßen aus und stimmt so auch 😉 :

Was viel eher falsch war, war meine Methode die Ableitung zu bilden. Daher konnte ich nie auf die eigentliche Funktion, mit der ich begonnen hatte, zurückkommen. Ich habe mich aber jetzt im Netz mal ein wenig schlauer gemacht und mir die Ableitung bilden lassen. Das ganze ist Schritt für Schritt erklärt und sieht so aus:

Powered by MATHDRAW
Summe ableiten: (f+g)‘ = f’+g‘
Powered by MATHDRAW
Produkt ableiten: (f*g)‘ =
… Weiterlesen “Integration von x*ln(x)”